解方程：

$$ \sin x +\sin 2x + \sin 3x = \cos x + \cos 2x +\cos 3x $$

找到的解法：稍微有点超纲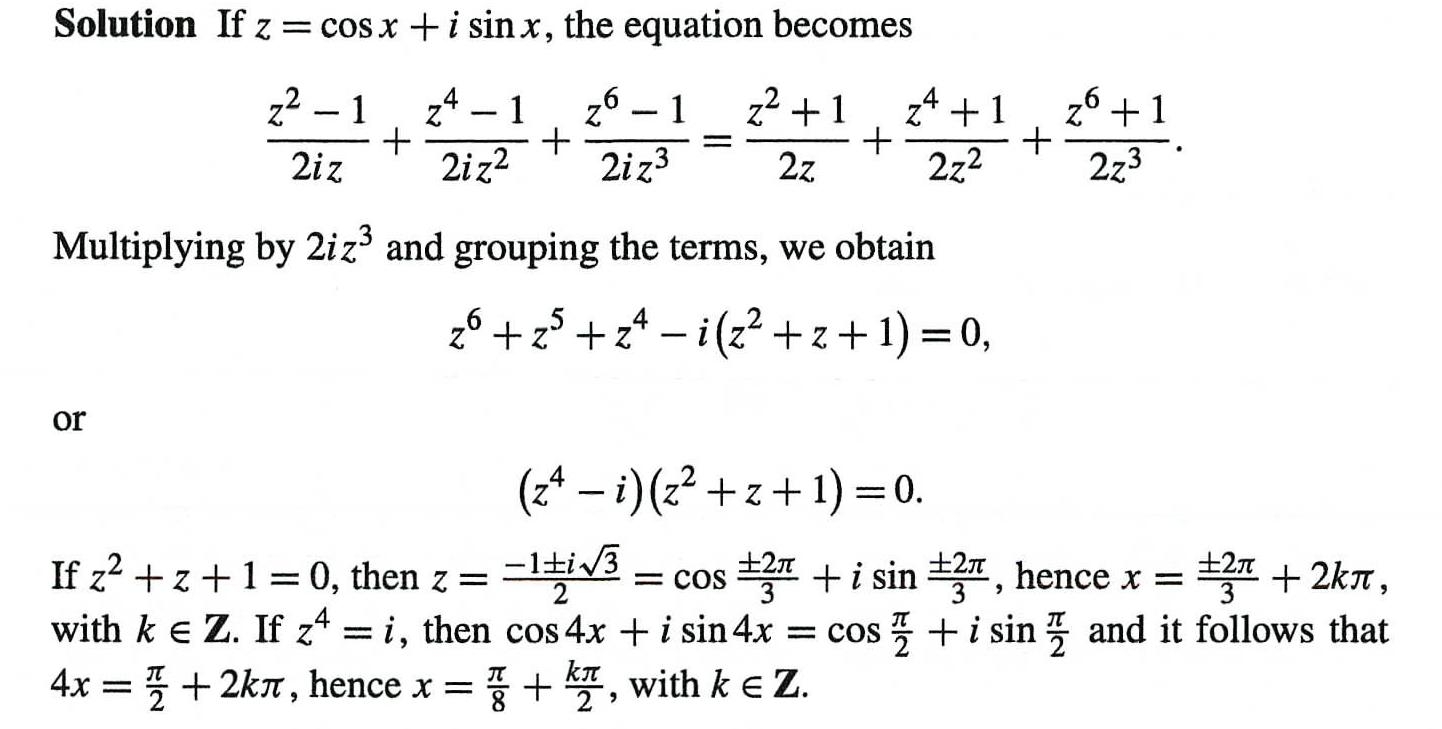

那就自己做一下吧：
两边有三项肯定不好解，浅用一下注意力 $(x+3x)/2=2x$，和差化积公式处理：

$$ \sin x + \sin 3x = 2 \sin 2x \cos x, $$

$$ \cos x + \cos 3x = 2 \cos 2x \cos x. $$

接下来就比较明了了，可以提取公因式：

$$ \sin 2x (2 \cos x + 1) = \cos 2x (2 \cos x + 1). $$

然后分类讨论：
$(i)$ 如果 $(2 \cos x + 1) \neq 0$，则可以两边同时除以 $(2 \cos x + 1)$，得到：

$$ \sin 2x = \cos 2x. $$

即

$$ \tan 2x = 1. $$

因此：

$$ 2x = \frac{\pi}{4} + k\pi \quad (k \in \mathbb{Z}), $$

$$ x = \frac{\pi}{8} + \frac{k\pi}{2} \quad (k \in \mathbb{Z}). $$

$(ii)$ 如果 $(2 \cos x + 1) = 0$，即：
$$\cos x = -\frac{1}{2}$$
则：

$$ x = \frac{2\pi}{3} + 2k\pi \quad \text{或} \quad x = \frac{4\pi}{3} + 2k\pi \quad (k \in \mathbb{Z}). $$

验证这些解是否满足原方程：

1. 对于 $(x = \frac{2\pi}{3} + 2k\pi)$：

   $$ \sin \frac{2\pi}{3} + \sin \frac{4\pi}{3} + \sin 2\pi = \frac{\sqrt{3}}{2} - \frac{\sqrt{3}}{2} + 0 = 0, $$

   $$ \cos \frac{2\pi}{3} + \cos \frac{4\pi}{3} + \cos 2\pi = -\frac{1}{2} - \frac{1}{2} + 1 = 0. $$

2. 对于 $(x = \frac{4\pi}{3} + 2k\pi)$：

   $$ \sin \frac{4\pi}{3} + \sin \frac{8\pi}{3} + \sin 4\pi = -\frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2} + 0 = 0, $$

   $$ \cos \frac{4\pi}{3} + \cos \frac{8\pi}{3} + \cos 4\pi = -\frac{1}{2} - \frac{1}{2} + 1 = 0. $$

因此，这些解均成立。
故，原方程的解为：

$$ \boxed{x = \frac{\pi}{8} + \frac{k\pi}{2} \quad \text{或} \quad x = \frac{2\pi}{3} + 2k\pi \quad \text{或} \quad x = \frac{4\pi}{3} + 2k\pi \quad (k \in \mathbb{Z})} $$

后记
与老师讨论了一下：

当然，在平时多练习一下这类题，训练思维也是很好的